习题精炼

Part 1

image.png

解：

x=at2，y=bt2，消去t得y=bx/a为直线运动，vx=dx/dt=2at，vy=dy/dt=2bt，所以物体做变速直线运动。

答案：B

Part 2

image.png 这一题因为印刷体问题看看就好。

速度是位矢对时间的一阶导数，加速度是速度对时间的一阶导数。

答案：D

Part 3

image.png

解：

\(\begin{aligned} &\begin{array}{l} a=\frac{d v}{d t}=4 t \\ d v=4 t d t \end{array}\\ &\int_{0}^{V} d v=\int_{0}^{t} 4 t d t\\ &v=2 t^{2}\\ &V=\frac{d x}{d t}=2 t^{2}\\ &\int_{x_{0}}^{x} d x=\int_{0}^{t} 2 t^{2} d t\\ &x=\frac{2}{3} t^{3}+x_{0} = 2.887 \mathrm{m} \end{aligned}\)

答案：A

Part 4

image.png

解：

\[\begin{aligned} &\frac{d v}{d t}=-k v^{2}\\ &\frac{d v}{v}=-k v d t &v=\frac{d x}{d t}\\ &\frac{d v}{v}=-k d x\\ &\int_{v_{0}}^{v} \frac{1}{v} d v=\int_{0}^{x}-k d x\\ &\ln v-\ln v_{0}=-k x\\ &v=v_{0} e^{-k x} \end{aligned}\]

Part 5

image.png

解：

\[\begin{aligned} &v=\frac{d x}{d t} \quad a=\frac{d v}{d t}\\ &\therefore a=v \frac{d v}{d x}=2+6 x^{2}\\ &v d v=\left(2+6 x^{2}\right) d x\\ &\int_{0}^{v} v d v=\int_{0}^{x}\left(2+6 x^{2}\right) d x\\ &\frac{1}{2} v^{2}=2 x+2 x^{3}\\ &v=2 \sqrt{x+x^{3}} \end{aligned}\]

Part 6

image.png

解：圆周运动的加速度分为切向加速度at和法向加速度an。

\(\begin{aligned} &a_{t}=\frac{d v}{d t}\\ &a_{n}=\frac{v^{2}}{R}\\ &a^{2}=d^{2} t+a_{n}^{2}\\ &\therefore a=\sqrt{\left(\frac{d v}{d t}\right)^{2}+\left(\frac{v^{2}}{R}\right)^{2}} \end{aligned}\)

答案：D

Part 7

image.png

解：

\(\begin{aligned} &v_{0}=1 \mathrm{m}\cdot s^{-1}\\ &\because v=1+t\\ &\therefore a=\operatorname{l m} \cdot s^{-2}\\ &s=2 \pi R\\ &v^{2}-v_{0}^{2}=2 a s\\ &v^{2}=8.2848 \mathrm{m} \cdot s^{-1}\\ &a_{n}=\frac{V^{2}}{R}=14.284 \mathrm{m} \cdot s^{-2} \end{aligned}\)

\(\begin{aligned} &v_{0}=1 \mathrm{m} \cdot s^{-1}\\ &a=\frac{d v}{d t}=1 \mathrm{m} \cdot s^{-2}\\ &v=\frac{d s}{d t}=1+t\\ &\therefore d s=(1+t) d t\\ &\int_{0}^{2 \pi R} d s=\int_{0}^{t} (1+t) d t\\ &t=\sqrt{4 \pi R+1}-1\\ &v=v_{0}+a t\\ &=\sqrt{4 \pi R+1}\\ &a_{n}=\frac{v^{2}}{R}=14.284 \mathrm{m} \cdot s^{-2} \end{aligned}\)

答案：E

Part 8

image.png

解：

\(\begin{aligned} &v=\frac{d s}{d t}=v_{0}-b t\\ &a_{t}=\frac{d v}{d t}=-b\\ &a_{n}=\frac{v^{2}}{R}=\frac{\left(v_{0}-b t\right)^{2}}{R}\\ &\therefore a=\sqrt{a_{t}^{2}+a_{n}^{2}}=\sqrt{b^{2}+\frac{\left(v_{0}-b t\right)^{2}}{R^{2}}}\\ &\begin{array}{l} \text { 方向与}\text {切线之间的}\text{夹角： } \\ \theta=\arctan \frac{a_{n}}{a_{t}}=\arctan \left[-\frac{\left(V_{0}-b t\right)^{2}}{R b}\right] \end{array} \end{aligned}\)

\(\begin{array}{c} a=b \\ \therefore\quad v_{0}-b t=0 \\ t=\frac{v_{0}}{b} \end{array}\)

\[\begin{aligned} t &=\frac{v_{0}}{b} \\ s &=\frac{v_{0}^{2}}{b}-\frac{1}{2} b \frac{v_{0}^{2}}{b^{2}} \\ &=\frac{v_{0}^{2}}{2 b} \\ \therefore n &=\frac{s}{2 \pi R}=\frac{v_{0}^{2}}{4 \pi R b} \end{aligned}\]

Part 9

image.png

解：

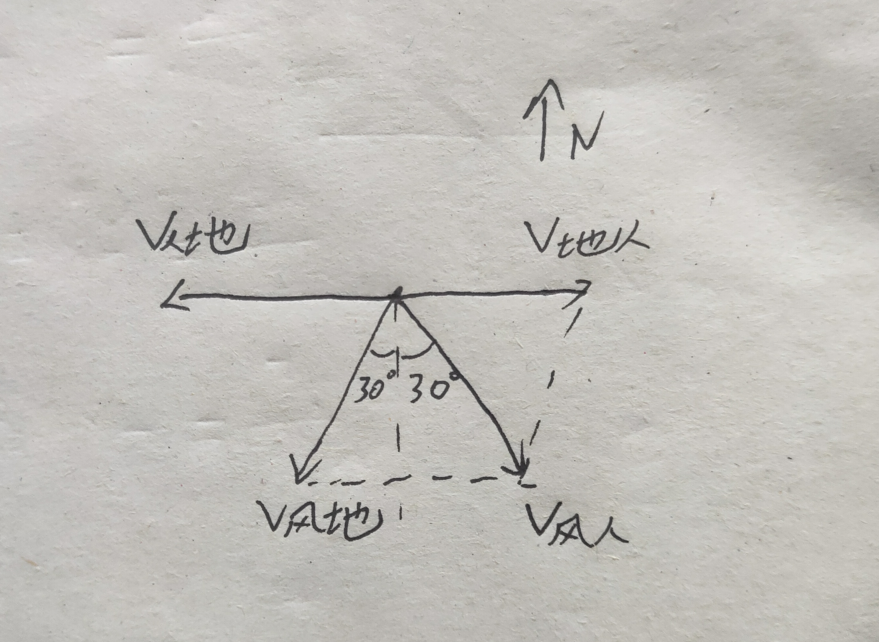
V风人 = V风地 + V地人 image.png

答案：C