复习
第一章 绪论
1.
作为基础性学科,它的任务是研究(地球形状)、(大小)及其(地球重力场);作为应用学科,它的任务是确立(地球参考坐标系)和(建立大地控制网),为地形测图和工程测量提供基础控制。
2.
大地测量学是通过在广大的地面上建立(大地控制网),精确测定大地控制网点的(坐标),研究测定地球形状、大小和地球重力场的理论、技术与方法的学科。
3.
大地测量学测量的精度等级(高),对局部的测量工作起到控制作用,为此需要研究更加精密的(测量仪器)、(测量方法)和(数据处理方法)。
4.解释大地测量学的概念及其与普通测量学的区别。
- 测量的精度等级更高,工作更加严密。
- 测量的范围更加广阔,常常是上百平方公里乃至整个地球。
- 侧重研究的对象不同。普通测量学侧重于研究如何测绘地形图以及进行工程施工测量的理论和方法。大地测量学侧重于研究如何建立大地坐标系、建立科学化、规范化的大地控制网并精确测定控制网点坐标的理论和方法。
5.解释大地测量学、大地控制点、大地控制网的基本概念。
- 大地测量学:大地测量学,又称为测地学。大地测量学是一门量测和描绘地球表面的科学。也就是研究和测定地球形状、大小和地球重力场,以及测定地面点几何位置的学科。
- 大地控制点:大地控制点简称“大地点”。经过大地测量在地面统一建立的控制点。具有统一精度的水平位置和高程的点。包括三角点、导线点、水准点。点上均埋设固定标志。
- 大地控制网:大地控制网简称“大地网”,是水平控制网与高程控制网的总称。
6.叙述应用大地测量学的基本任务及其重要作用
- 任务:通过实地观测和数据处理,精密确定控制点在全区域统一 坐标系中的空间位置和重力场参数,并监测这些控制点随时间的变化量,这就是应用大力测量学的基本任务。
- 作用:为地形测图提供控制基础;为城乡建设和矿山工程测量提供起始数据;为地球科学的研究提供信息;在防灾、减灾和救灾中的发挥作用;发展空间技术和国防建设的重要保障;在气象预报、地球温室效应和海洋与大气污染等环境监测中的发挥作用。
7.了解大地测量学的基本内容、分类以及发展史。
- 基本内容:大地测量学,又称为测地学。大地测量学是一门量测和描绘地球表面的科学。也就是研究和测定地球形状、大小和地球重力场,以及测定地面点几何位置的学科。它也包括确定地球重力场和海底地形,是测绘学的一个分支。
- 分类:
- 几何大地测量学:它的基本任务是确定地球的形状和大小及确定地面点的几何位置。
- 物理大地测量学:它的基本任务是用物理方法(重力测量)确定地球形状及其外部重力场。
- 空间大地测量学:主要研究人造地球卫星及其他空间探测器为代表的空间大地测量的理论,技术与方法。
8.简述应用大地测量学有哪些分支。
- 大地测量的基本知识。
- 大地坐标系统的建立与坐标系统的转换。
- 大地测量基本技术与方法。
- 地面控制网的建立。
- 数据处理。
第二章 大地测量基本知识
1.
在野外测量整置仪器时,使仪器垂直轴与通过地面点的(铅垂线)一致。由此可见,它是野外测量工作的基准线。处于静止状态的液体表面处处与重力方向正交,这静止的液体表面称为(水准面)。
2.
在不同测站上观测的水平角就是在高低不同的(水准面)上的角度,水准测量所测得的两点间的高差,是过这两点的不同水准面间的(铅垂线)长度;可见,(水准面)就是野外测量工作的基准面。
3.
选择一定(形状)和(大小)的椭球后,将以大地水准面为基准面的野外观测成果换算到这个椭球面上,在它上面计算点位坐标。要做到这一点,还必须将它与大地水准面的(相关位置)确定下来,这项工作称为(椭球定位)。
4.
(参考椭球面)是测量计算的基准面,(椭球面法线)则是测量计算的基准线。
5.
由于大地水准面与椭球面不可能处处(重合),两者距离为(N)。在同一测站点上(铅垂线)与椭球面法线也不会重合,两者之间的夹角称为垂线偏差。
6.
(垂线偏差)和(大地水准面差距)对确定天文坐标与大地坐标的关系、地球椭球的定位以及研究地球的形状和大小等问题有着重要的意义。
7.
PQ的天文坐标方位角是指,过P点(铅垂线)和另一地面点Q所作的垂直面与过P点的天文子午面的夹角,从P点的正北方向起始由0~360°(顺时针)方向量取。
8.
P点和另一地面点Q点的大地方位角是指,P点的子午面与过P点(法线)及Q点的平面所成的角度,由子午面顺时针方向量起。
9.
站心地平直角坐标系是指,原点位于地面(测站点P),z轴指向测站点的椭球面法线方向,又称大地(天顶方向),x轴是原点的大地子午面和包含原点且和法线垂直的平面的交线,指向(北点方向),y轴与x、z轴构成(左手坐标系)。
10.
以(原子时秒长)定义的世界时为协调世界时,简称(UTC)。由于原子时快于世界时,协调世界时每年要(跳秒),才能保证时分秒与世界时一致。
11.
由于重力等位面上各点的重力不同,两个重力等位面之间的距离也不同。即说明重力位水准面之间既不(平行)也不(相交)和(相切)。与平均的海水面最接近的重力等位面称为(大地水准面)。
12.
正常重力位是一个不涉及地球(形状)和(密度),函数较为简单可直接计算得到的近似的(地球重力位)。正常重力位是对应于正常椭球所产生的重力位。引入正常椭球后,地球的重力位被分成(正常重力位)和(扰动位)。
13.
水准测量是沿着水准面进行的,两点间的高差应该是通过两点的两个(水准面)之间的差距。由地球重力场基本理论可知,水准面是(重力等位面),即在同一水准面上各点的重力位能都相等。
14.
由于地面上的重力加速度随纬度和物质分布的情况而变化,由此可见,水准面相互间是(不平行的),这是水准面的特性。这种特性是由两部分原因造成,即不同的地方,其(正常重力加速度)与(重力异常)是有别的。
15.
由于相邻水准面的不平行性能,使得水准测量中所经过的路线不同,测得的高差也不同,造成水准测量结果的(多值性)。即使水准测量中没有误差,闭合环线的高差闭合差也不会等于零。在闭合的环形水准路线中,由于水准面不平行所产生的闭合差称为(理论闭合差)。
16.
似大地水准面不具备水准面的性质,正常高确乏物理意义。似大地水准面只是用于计算的辅助面。但是似大地水准面与大地水准面相差甚微,在平均海水面上为(0),在平原地区只有(几厘米),高原地区最大差异达(3 m)。所以正常高的数值与正高很接近,又能精确计算求得,故在实际工作中具有重要意义。因此,我国规定采用(正常高高程系统)作为我国的统一高程系统。
17.
水准原点在1956年黄海高程系统的高程值(72.289米),以1985国家高程基准为准的高程值(72.260米)。
18.名词解释
- 大地水准面:大地水准面是指与平均海水面重合并延伸到大陆内部的水准面。
- 大地体:由大地水准面所包围的地球形体,称为大地体。
- 垂线偏差:垂线偏差是指同一测站点上铅垂线与椭球面法线之间的夹角u。
- 大地水准面差距:大地水准面差距是从大地水准面上的点沿地球椭球法线到地球椭球的距离。
- 天文方位角:天文方位角又称“真方位角”。从地面上某点的真子午线按顺时针方向至另一目标方向线的水平角。
- 大地方位角:大地方位角,即方位角。一条直线的方位角是指从标准方向的北端起,顺时针方向量至该直线的角度。
- 春分点:春分点,是指太阳从南向北在黄赤道上的交点。
- 世界时:格林尼治的平太阳时(从半夜零点算起)定义为世界时(UT)。
- 协调世界时:以原子时秒长定义的世界时为协调世界时(UTC)协调世界时秒长为原子时,但表示时间的年月日时分秒仍是世界时。由于原子时快于世界时,UTC每年要跳秒,才能保证时分秒与世界时一致。
- 原子时:以物质内部原子运动周期(如色原子133能级辐射震荡频率9192631170周为一秒)定义原子时(IAT),原子时起点定在1958年1月1日0时0分0秒(UT2),即在此时刻原子时与世界时重合。但事后发现,原子时与世界时此刻之差为0.0039秒,此后,原子时与世界时之差便逐年积累。
- 重力位水准面:重力位相等的面称为重力等位面,即通常所说的水准面。
- 正常重力位:是一个函数简单、不涉及地球形状和密度便可直接计算的得到的地球重力位的近似值的辅助重力位。
- 水准测量的理论闭合差:如果不考虑仪器本身的误差与观测误差,由同一起始水准点出发,由几何水准测量经不同的水准线路测量同一未知点的高程是不相同的,换句话说,由同一起始点测量水准闭合环线的高程闭合差不等与零,其闭合差称为水准理论闭合差。
- 大地水准面:大地水准面是指与平均海水面重合并延伸到大陆内部的水准面。
- 似大地水准面:从地面点沿正常重力线量取正常高所得端点构成的封闭曲面。
- 高程系统:高程系统是指相对于不同性质的起算面(大地水准面、似大地水准面、椭球面等)所定义的高程体系。
- 正高:正高是以大地水准面为基准的高程,即地面点到大地水准面的铅垂距离。又称为绝对高程或者海拔,简称高程。
- 正常高:地面点沿铅垂线到似大地水准面的距离称为正常高。
- 大地高:大地高是地面点沿参考椭球面法线到参考椭球面的距离,大地高一般用符号H表示。
- 高程异常:高程异常是似大地水准面与参考椭球面之间的高差。
19.简述参考椭球的定位和定向。总地球椭球满足哪些条件。
- 简述:参考椭球的定位和定向,就是依据一定的条件,将具有确定参数的椭球与地球的相关位置确定下来。
- 条件:
- (1)椭球质量等于地球质量,两者的旋转角速度相等。
- (2)椭球体积与大地体体积相等,它的表面与大地水准面之间的差距平方和为最小。
- (3)椭球中心与地心重合,椭球短轴与地球平自转轴重合,大地起始子午面与天文起始子午面平行。
20.地心坐标系.参心坐标系和站心坐标系是如何建立的,简述他们之间的转换模型。
- 地心坐标系:地心坐标系以地球质心为原点建立的空间直角坐标系。地心坐标系是在大地体内建立的O-XYZ坐标系。原点O设在大地体的质量中心,用相互垂直的X,Y,Z三个轴来表示,X轴与首子午面与赤道面的交线重合,向东为正。Z轴与地球旋转轴重合,向北为正。Y轴与XZ平面垂直构成右手系。
- 参心坐标系:参心坐标系是以参考椭球的几何中心为基准的大地坐标系。参心空间直角坐标系是在参考椭球内建立的O-XYZ坐标系。原点O为参考椭球的几何中心,X轴与赤道面和首子午面的交线重合,向东为正。Z轴平行于地球质心指向地极原点的方向,向北为正。Y轴与XZ平面垂直构成右手系。
- 站心坐标系:站心坐标系是以测站为原点的坐标系。
- 站心地平直角坐标系:以站心(如GPS接收天线中心)为坐标系原点O,Z轴与椭球法线重合,向上为正(天向),y与椭球短半轴重合(北向),x轴与地球椭球的长半轴重合(东向)所构成的直角坐标系,称为当地东北天坐标系(ENU)。
- 站心极坐标系:以站心为坐标极点O,以水平面(即xoy平面)为基准面,以东向轴(即x轴)为极轴,ρ为卫星到站点的距离,az为星视方向角(azimuth angle),el为星视仰角(elevation)。
转换模型:
21.重力位水准面如何定义大地水准面。简述水准面的不平行给测量带来哪些困难。
- 与平均的海水面最接近的重力等位面称为大地水准面。
- 由于不同高程的水准面不平行,沿不同路线测得的两点间高差将有差异
22.利用公式和图示描述某一点的大地高.正高和正常高之间的关系。

B点为正高,A点为正常高,O点为大地高,大地高是以地球椭球面为基准面。地面任点的正常高是指该点沿法线方向至似大地水准面的距离。
第三章 大地测量控制网的建立
1.
我国建立平面控制网的经典方法主要是(三角测量法),辅助方法有导线测量法、(三边测量法)和(边角同测法)。
2.
根据测图要求,首级解析图根点对于起算三角点的点位中误差,在实地不得超过(0.1M mm (M为测图比例尺分母))。
3.
由于图根点的误差不仅来源于图根点本身的(测量中误差),而且含有起算三角点的(点位中误差)。通常规定相邻三角点的点位中误差,应小于图根点点位中误差的(1/3)。
4.
三角网中的边长愈短,三角点的密度就(愈大),三角点的密度,主要根据(测图方法)及(测图比例尺)而定。
5.
(一等)水准网点是国家高程控制网的骨干,同时也是研究地壳和地面垂直运动海面变化和不同海面差异以及有关科学问题的主要依据。(一等)和(二等)水准网统称国家精密水准网。
6.
各等级水准网的精度指标是按照每公里高差中数中误差来衡量的,包括(偶然中误差)和(全中误差),它们的公式分别为:


7.
每公里高差中数的偶然中误差是由(测段往返测高差不符值)计算的;每公里水准测量高差中数的全中误差是由(水准环线闭合差)计算的。
8.
我国的黄海高程基准是采用了(平均海水面)作为参考面的高程基准。在1956年黄海高程系中,青岛水准原点的高程为(72.289)m。在1985年国家高程系中,青岛水准原点的高程为(72.260)m。
9.
我国大陆地区已经布设了4个大规模的全国GPS网,它们是国家测绘部门建立的(全国 GPS A、B级网),(全国 GPS 一、二级网),攀登计划项目和(现代地壳运动与地球动力学研究)布设的GPS监测网和国家重大科学工程(中国地壳运动观测网络)的三级GPS网。
10.
我国第一个国家重力控制网称为(“国家57重力基本网”),该网由27个(基本点))和82个一等点组成。57网没有绝对重力点,通过联测前苏联重力网引入,属于(波茨坦重力基准)。
11.
80年代初,我国又更新建立了(“国家84重力基准网”),该重力系统是由国家85重力基本网中的绝对重力点所定义的,由6个(基准重力点)、46个(基本重力点)和5个(引点)组成。
12.
我国自前至后供使用的重力基准网有:(国家57重力基本网)、(国家84重力基准网)和(国家2000重力基准网)。
13.
2000国家重力基准网由22个(基准点)和126个(基本点)组成,还包括若干(重力基线和(重力引点),并改造国内现有的9条重力基线。
14.
根据工程建设对工程控制网提出的不同要求,工程控制网一般可分为三类:(测图控制网)、(施工控制网)和(变形监测网)。
15.
分析对于1/20 00比例尺测图,首级解析图根点相对于起算三角点的点位中误差不得多于(0.2 m),次级三角点的点位中误差不得多于(0.07 m)。
16.
城市和工程测量控制网的布设方案有(三角网)、(三边网)、(导线网)、(GPS网)等形式。实际应用中,首级控制网以(GPS网)的布设为主要形式,次级加密网有(GPS网)、(导线网)等多种形式。
17.
测距精度表达式 m=±(a+bxD) 中,a 的单位是(mm),表示的意义是(固定偏差);b的单位是(ppm),表示的意义是(比例误差)。
18.
对于单一方位坐标附合导线,最弱点位于(中点)。单一闭合或附合水准路线最弱点高程中误差计算公式为:
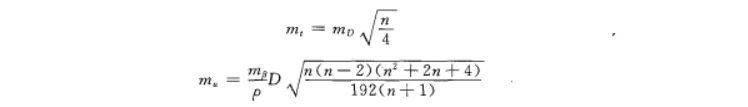
19.
等权代替法的实质是,将复杂的水准网通过(路线合并)与(路线连接),简化成一条虚拟的等权路线,以便按单一路线计算最弱点高程中误差。
20.
城市或工程GPS网的相邻点边长精度计算公式如下。其中,σ为(标准差);a为(固定误差);b为(比例误差系数);D为(相邻点间距离)。 \(\sigma=\sqrt{a^{2}+(b D)^{2}}\)
21.
水准测量的精度根据往返测的(高差不符值)来评定,由n 个测段往返测的高差不符值▲计算每公里单程高差的偶然中误差(相当于单位权观测中误差)公式为: \(\mu=\pm \sqrt{\frac{\frac{1}{2}\left[\frac{\Delta \Delta}{R}\right]}{n}}\)
22.国家大地控制网的布网原则。
- 分级布网,逐级控制
- 保持必要的精度
- 应有一定的密度
- 应有统一的规格
23.叙述国家水准控制网的布网原则及其作用。
原则:
- 从高级到低级
- 从整体到局部
- 逐级控制
- 聚集加密
作用:在全国范围内,测定一系列统一而精确的地面点高程,为测制各种比例尺地形图提供高程 制基础;为水利、工程建设和科学研究提供资料。
24.水准网的精度指标有哪些,并表达出其数学公式。
各等级水准网的精度指标是按照每公里高差中数中误差来衡量的,包括偶然中误差和全中误差 。


25.简述国家GPS网有哪些类型。简述四种国家GPS网的作用。
类型:
- 国家 GPS A、B级网
- 全国 GPS 一、二级网
- 攀登项目 GPS 网
- 中国地壳运动观测网络
作用:
- 监测研究地壳形变与块体运动
- 检核和加强各地区天文大地网,建立统一的高精度大地基准
- 建立地心参考系,精确确定参心坐标系与地心坐标系之间的转换参数
- 精化大地水准面等等
- 同时这些全国网的建立与复测都可以成为建立我国新一代高精度地心参考系、监测和研究地壳运动的基础。
26.工程控制网有哪些类型,它们的布网各有哪些特点。
工程控制网分为:测图控制网 施工控制网 变形监测网。
- 测图控制网:能使测量误差的累积得到控制,保证了图纸上所测绘的内容(如地形、地物等)精度均匀,使相邻图幅之间准确拼接。
- 施工控制网:用于工程施工放样,具有一定的精度。
- 变形监测网:基准网点位选择在坚固而稳定的地面或建筑物顶上,具有较高的精度。
27.叙述大地测量中控制网技术设计的详细内容。
- 收集资料
- 地形图、大地测量成果资料(三角测量、导线测量、GPS测量、水准测量的点之记、成果表、技术总结、控制网略图及水准路线图,原有点位的觇标、标石的保存情况等 )交通图、气象资料
- 实地踏勘
- 现状和已有点位情况
- 图上设计
- 拟定控制点的点位和网形,方法:
- 把测区中、小比例尺地形图拼接起来,在其上绘出测区的范围,标明已知的高等级控制点的位置。
- 选定待测控制点并连接成一定的网形。注意:
- 旧有控制点的位置适宜,应尽量与旧点重合。从已知点开始逐点向外扩展,直至选取的控制点均匀布满整个测区为止。
- 相邻点间连接而成的网形结构应合乎规范相应等级的要求。
- 网形:三角网、三边网、导线网、GPS网。
- 点位要求
- 三角网、三边网控制点间要相互通视,导线网只要求相邻点间相互通视,GPS网点间不要求相互通视,但对于使用全站仪进行进一步加密的导线测量,为保证导线测量有起算的方位角,GPS网布设时应注意导线两端位置有互相通视的两个点。
- 进行点位、边长、方位角的精度估算
- 最重要的是最弱点点位位置和最弱边边长的精度估算。
- 复查
- 检查的项目有设计的点位数量、质量是否合乎规范的要求;控制点之间是否通视;布设的项目是否齐全等。
- 拟定控制点的点位和网形,方法:
- 写出控制网技术设计书
- 设计书的内容包括:测量任务,测区范围测区的自然地理、气象、交通情况,作业依据,旧有资料及其利用情况,新网的起算数据、布设等级、点的数量和网形结构、精度估算结果。对于三角网则应有觇标高度和类型设计、仪器装备和各项器材的计划数量、观测与数据处理方案和最终提供的成果。
- 上交资料
- 应提交控制网设计图纸以及控制网技术设计说明书。
28.详细叙述控制网的精度估算的主要步骤。
29.等权代替法的实质是什么。
等权代替法的实质是将复杂的水准网通过路线合并与路线连接,简化成一条虚拟的等权路线,以便按单一路线计算最弱点高程中误差。
设三条路线长分别为L1、L2、L3,则
- 三个高差观测值权分别为 P1=1/L1、P2=1/L2、P3=1/L3
- 结点的权 P=P1+P2+P3
- 相应的等权路线长度为L=1/P
- 结点的高程中误差为
\(M_{H}=M_{W} \sqrt{\frac{1}{P}}\)
Mw为每千米高差全中误差
30.简述GPS网的设计基准和观测刚要。
- 联测测区附近高等级的具有WGS-84坐标的控制点,通过GPS观测数据处理,GPS点能够得到高精度的WGS-84坐标。
- 联测一定数量高等级的国家或地方坐标系的控制点,联测一定数量的水准高程点。
- 联测点三个以上,且分布均匀。
- GPS网形设计完成后,要到实地选定点位并埋设标石。点位选定要求周围高度角15°以上不应有障碍物,点位附近不应有强的电磁波辐射源。根据设计的GPS网形和精度等级,确定观测时间段的长度,制定观测实施计划。GPS网设计的最后部分应提出用何种软件进行数据处理的方法以及最终提供的成果。
第四章 大地测量观测技术
1.
方向观测法中,观测的起始方向常称为(零方向)。当方向数不超过3个时,由于半测回持续时间较短,可以(不归零)。此时,方向观测法也就是(测回法)。
2.
方向观测法中,每一测站点均应进行多测回观测,其测回数目取决于测量(等级)和选用的(仪器)。
3.
一个测回内2c互差或同一方向的测回互差超限时,应重测超限方向并(联测零方向)。
4.
通过(盘左、盘右观测)可以消除指标差对垂直角的影响,但是在垂直角的观测过程中仍需要计算指标差。因为在较短观测时间内,指标差可视为(常数)。如果其值稳定,则说明观测误差较小;如果其值变化范围较大,超出限差规定,则说明观测结果存在较大的误差影响,应予(重测)。
5.
电磁波测距是通过测定电磁波在待测距离上往返(传播时间),进而确定待测距离D,公式为:
6.
全站仪的精度是由(测角)精度和(测距)精度共同决定的。其精度等级设计时,采用(等影响)原则。
7.
在光电测距误差分析中,比例误差的分类:(真空中光速C0的误差)、(大气折射率n的误差 )和(调制频率f的误差)。
8.
测距成果的换算包括(斜距换算至标石中心的改正–归心改正 )、(斜距化成平距的计算)、(平距化至椭球面的计算)。
9.
对于同一视线高度,水准尺上的(基本分划与辅助分划的读数之差),叫做基辅差,也称为(尺常数)。
10.
在二等水准路线主要技术要求中,测段路线往返测高差不符值是( ±4√K ),附合路线闭合差( ±4√L ),以S1数字准仪为例,在观测中要求下列的限差为多少。
11.
在三轴误差中,(视准轴误差)和(水平轴倾斜误差)可以在盘左.盘右读数的平均值中得到抵消,但(垂直轴倾斜误差)在盘左.盘右观测结果的平均值中不能消除。
12.
测距仪(全站仪)的标准精度一般为2+bppm,其中2为(固定误差),b为(比例误差)。
13.
利用三角高程进行精密高程测量时,为了较好消除大气折射误差,通常采用(对向观测)方法。
14.
用光电测距仪进行精密距离测量时,在测站上一般应对测得的倾斜距离加入:(象改正)、(仪器常数改正)、(频率改正)、归心改正.周期误差改正。
15.
衡量水准测量外业观测的两个精度指标分别是(偶然中误差)和(全中误差)。
16.
精密水准测量中每个测段要求偶数测站可消除(两水准尺零点差)的影响。
17.名词解释
- 仪器加常数:对于全站仪和测距仪来讲,在使用仪器对目标(反射棱镜)进行测距时,光波通过全反射棱镜玻璃通过的距离的延长与实际定义的测距点有一定的误差。加常数就是改正这种测距误差
- 视差:由于望远镜对光不完善,目标的像与十字丝板没有重合,当观测者的眼睛.上下移动时,目标的像与十字丝有相对移动,这种现象称为视差。
- 垂直轴误差:垂直轴与铅垂线不重合
- 大气微分折光:线通过密度不均匀的空气介质时,经过连续折射后形成一条曲线,并向密度大的一方弯曲。实际照准方向与理想的照准方向有一微小交角,称为微分折光
- 大气水平折光:在水平面上的分量,称为大气水平折光,它将影响水平方向的观测精度
- 大气垂直折光:微分折光在铅垂面上的分量称为大气垂直折光,它将影响垂直角观测精度
- 竖盘指标差:当视线水平且竖盘水准管气泡居中时的竖盘读数与应有的竖盘指标正确读数(即90°的整倍数)有一个小的角度差x,称为竖盘指标差,即竖盘指标偏离正确位置引起的差值。采用盘左、盘右位置观测取平均计算得竖直角,消除竖盘指标差的影响
- 垂直角互差:同一方向,由各测回各丝所测得的全部垂直角相比较,测角三角高程,J2级仪器,四等不超过10″,测距高程测量时,J2级仪器不超过7″。
- 指标差互差:单独方向连续观测时,各测回同一根水平丝所算得的结果互相比较,测角三角高程,J2级仪器,四等不超过15″,测距三角高程时,J2级仪器不超过7″。分组观测时,仅在一测回内各方向按同一根水平丝所算得的结果互相比较。
- 对向观测法:通过观测两点间的水平距离和天顶距(或高度角)求定两点间高差的方法。
18.叙述精密测角的一般原则及其消除哪些误差。
- 将测段的测站数安排成偶数,消除视准轴与水准轴不平行的误差。
- 在实际水准测量作业中各测段的测站数目安排成偶数,且在相邻测站上使两水准尺轮流作为前视尺和后视尺,消除水准尺长度误差的影响。
- 采用 “ 后前前后 ” 的观测程序,消除仪器和水准尺(尺台和尺桩)垂直位移的影响。
- 前后视距尽量相等,并使视线离地面有足够的高度,在坡度较大的水准路线上进行作业时应适当缩短视距,消除大气垂直折光的影响。
- 在布设与输电线平行的水准路线时,必须使水准路线离输电线 50cm 以外,如果水准线路与输电线相交,则其交角应为直角,并且应将水准仪严格地安置在输电线的下方,标尺点与输电线成对称布置,消除电磁场对水准测量的影响。
19.方向观测法的观测流程和注意事项。
方向观测法是在一测回内将测站上所有要观测的方向先置盘左位置,逐一照准进行观测,再盘右位置依次观测,取盘左、盘右平均值作为各方向的观测值。测站点O周围有待定的目标A、B、C、D、E,首先选择其中一个方向(如A)作为起始方向。用盘左位置顺时针方向旋转照准部,依次照准A、B、C、D、E、A,读取观测值,称为上半测回;然后纵转望远镜,用盘右位置逆时针方向旋转照准部,仍从A开始,依次照准A、E、D、C、B、A并读数,称为下半测回。上、下两个半测回合起来称为一个测回。
观测的起始方向常称为零方向。要求每半测回观测闭合到零方向的目的在于检测观测过程中水平度盘有无方位变动,此时上、下半测回均构成一个闭合圆,所以这种观测又成为全圆观测法,这种闭合操作称为“归零”。当方向数不超过3个时,由于半测回持续时间较短,可以不归零。方向数只有2个时,方向观测法也就是测回法。
20.相位式测距仪测距的求距基本公式和基本原理是什么。
基本公式是:D=u(N+ΔN)其中ΔN=Δφ/2π
基本原理是:通过测量连续的调制信号在待测距离上往返传播产生的相位变化来间接测定传播时间,从而求得被测距离。
N值确定方法:当测尺长度u大于距离D时,N=0。为了扩大单值解的测程,必须选用较长的测尺,即选择较低的调制频率。根据u=λ/2=c/2f,取c=3³103,可算出测尺长度相应的调制频率。
21.电磁波测距原理和误差来源。
电磁波测距有两种方法:脉冲测距法和相位测距法。
- 脉冲测距法:由测线一端的仪器发射的光脉冲的一部分直接由仪器内部进入接收光电器件,作为参考脉冲;其余发射出去的光脉冲经过测线另一端的反射镜反射回来之后,也进入接收光电器件。测量参考脉冲同反射脉冲相隔的时间t,即可由下式求出距离D: ,式中 c为光速。卫星大地测量中用于测量月球和人造卫星的激光测距仪,都采用脉冲测距法。
- 相位测距法:用高频电流调制后的光波或微波从测线一端发射出去,由另一端返回后,用鉴相器测量发射波与回波之间的相位差。若调制频率为f,则电磁波往返经历的时间为: ,式中n是时间t中的整周数。将 t代入到上列脉冲测距法的公式中,得距离D为: ,式中λ是已知的调制波波长相当于测量距离的尺子的长度,n相当于测程上的整尺数是不足一个测尺长的尾数。 为了确定整尺数n,通常采用可变频率法和多级固定频率法。前者是使测距仪的调制频率在一定范围内连续变化,这就相当于连续改变测尺长度,使它恰好能量尽待测距离。测距时,逐次调变频率,使不足整尺的尾数等于零。根据出现零的次数和相应的频率值,就可以确定整测尺数n°当采用多级固定频率法时,相当于采用几根不同长度的测尺丈量同一距离。根据用不同频率所测得的相位差,就可以解出整周数n,从而求得距离D。
主要误差来源有:视距丝在标尺上的读数误差、标尺不竖直的误差、垂直角观测的误差及大气折射光影响等。
22.何谓水平折光差?为什么说由它引起的水平方向观测误差呈系统误差性质?在作业中应采取什么措施来减弱其影响?
线通过密度不均匀的空气介质时,经过连续折射后形成一条曲线,并向密度大的一方弯曲实际照准方向与理想的照准方向的微小夹角叫做微分折光,其在水平方向的投影叫做水平折光差。 微分折光的水平分量影响着视线的水平方向,对精密测角的观测成果产生系统性质的误差影响。
在测量工作中,选点要注意使视线保持足够的高度,应避免使视线靠近山坡,大河或与湖泊的岸线平行并应尽量避免视线通过高大建筑物,烟囱和电杆等实体的侧方。在水平折光差影响大的地区要适当的缩短边长,不要在容易形成空气密度分布不均匀的时间里观测。
23.精密水准测量遵循的一般原则及其消除的误差有哪些。
- 将测段的测站数安排成偶数,消除视准轴与水准轴不平行的误差。
- 在实际水准测量作业中各测段的测站数目安排成偶数,且在相邻测站上使两水准尺轮流作为前视尺和后视尺,消除水准尺长度误差的影响。
- 采用“后前前后”的观测程序,消除仪器和水准尺(尺台和尺桩)垂直位移的影响。
- 前后视距尽量相等,并使视线离地面有足够的高度,在坡度较大的水准路线上进行作业时应适当缩短视距,消除大气垂直折光的影响。
- 在布设与输电线平行的水准路线时,必须使水准路线离输电线50cm以外,如果水准线路与输电线相交,则其交角应为直角,并且应将水准仪严格地安置在输电线的下方,标尺点与输电线成对称布置,消除电磁场对水准测量的影响。
24.分析光电测距精密三角高程测量的基本原理和误差来源与影响。
如果在A点设站观测B点,测得倾斜距离d和垂直角α,则可以计算测站点至照准点的高差。设A点的仪器高为i,B点的觇牌高为v,则高差的计算公式为:
\[h=d \cdot \sin \alpha+\frac{1-K}{2 R} d^{2} \cos ^{2} \alpha+i-v\]式中 d—经过各项改正后的倾斜距离;Α—观测的垂直角,R—测区处的地球椭球平均曲率半径,I—仪器垂直度盘中心至地面点的高度,V—觇牌中心至地面点高度,K—大气垂直折光系数。
- (1)测距误差mD对高差的影响与垂直角α的大小有关。一般中短程光电测距仪或全站仪的测距精度mD=(5+5ppmD)mm,它对高差精度的影响很小。
- (2)测角误差mα对高差的影响随着水平距离的增加正比例增大,其影响远远超过测距误差,是制约高差精度的最主要误差源。
- (3)大气垂直折光误差mk,如果在相同的时间对向观测垂直角,可认为K1=K2,这就抵偿了大气垂直折光对高差中数的影响。但是事实上,对向观测难以同时进行,对向大气垂直折光的影响也不会完全一样,往测和返测时 值总会存在差异,所以对向观测时mk应是往返测大气垂直折光系数K值变化的影响。 大气折光差对所测高差的影响随着距离的增加而急剧增大,在1km范围以内,它的影响不大。
- (4)量高误差mi和mv对观测高差的呈系统性,作业时量取仪器高和觇牌高各两次并取中数。
第五章 地球椭球与测量计算
1.
用椭球来表示地球必须解决2个问题:一是(椭球参数的选择); 二是(确定椭球与地球的相关位置),即椭球的定位。
2.
旋转椭球常用的五个基本几何参数是:(长半轴a)、(短半轴b)、扁率α、(第一偏心率e)、第二偏心率e′。描述地球椭球常用的四个参数是(椭球长半径)、(引力常数与地球质量的乘积)、(地球重力场二阶带球谐系数)、(地球自转角速度)。
3.
通常垂线偏差通常小于(10″ ),由天文方位角归算大地方位角的计算公式(A=α-(λ-L)sinφ),此公式称之为拉普拉斯方程式。
4.
利用大地原点的(大地经纬度L0)、(B0)、(大地方位角a0)和(大地高H0)作为大地起算数据,依据归算到椭球面上的方向和边长观测值,在椭球面上进行各种计算和平差,就可得到天文大地网中各点的大地经纬度。所以,大地原点也可称为(大地起算点或大地基准点)。
5.
包含椭球面上一点的法线,可作(无数)个法截面,相应就有(无数)个法截线。椭球面上法截线的曲率半径不同于球面上的法截线(大圆弧)曲率半径都等于圆球的半径,而是除(两极)外,椭球面上任意一点的法截线,随着它们的方向不同,每条法截线在该点的(曲率半径)不相同。
6.
将地面观测方向归算至椭球面上,包括三个基本内容:一是(垂线偏差改正);二是(标高差改正);三是(截面差改正)。
7.
垂线偏差改正数的大小主要取决于测站点的(垂线偏差)和观测方向的(天顶距)。仅在国家() 一、二)等三角测量计算中,才规定加入此项改正。
8.名词解释
- 子午圈 :包含旋转轴的平面与椭球面相截所得的椭圆称为子午圈。
- 卯酉圈 :就是指地平坐标系中的大圆。即与子午圈相垂直的地平经圈 ,它与地平圈相交于东点和西点。
- 绝对垂线偏差 垂线与总地球椭球法线构成的角度称为绝对垂线偏差
- 相对垂线偏差 垂线与参考椭球法线构成的角度称为相对垂线偏差
- 法截面 :过椭球面上任意一点可作一条垂直于椭球面的法线,包含这条法线的平面叫做法截面。
- 法截线 :法截面同椭球面的截线叫法截线。
- 平均曲率半径 :所谓平均曲率半径,就是过椭球面上—点的所有法截线。
- 主曲率半径 :在微分几何中,曲面上任一点的切平面上,都存在着2个互相垂直的特殊方向,使法截线的曲率达到最大值和最小值。这2个方向称为主方向,其相应的法截线曲率称为主曲率,法截线曲率半径称为主曲率半径。
- 正法截线 :当法截线 偏南,法截线 偏北。称 为 点的正法截线。
- 反法截线 :当法截线 偏南,法截线 偏北。称 为 点的反法截线。
- 大地线 :椭球面上两点间的最短程曲线叫做大地线。
- 垂线偏差改正 :为了求得椭球面上以法线为基准的水平方向观测值,必须对野外观测的水平方向观测值加入相应的改正数,称为垂线偏差改正。
- 标高差改正 :当进行水平方向观测时.如果照准点高出椭球面某一高度,则照准面就不能通过照准点的法线同椭球面的交点,由此引起的方向观测值的改正叫做标高差改正。
- 截面差改正 :应当用两点间的大地线代替相对法截线。这样将法截线方向换算为大地线方向应加的改正叫截面差改正。
- 大地元素 :椭球面上点的大地经度 、大地纬度 、两点间的大地线长度 及其正反大地方位角 、 ,通称为大地元素。
- 大地问题解算 :如果知道某些大地元素推求另外一些大地元素,如根据大地测量成果(角度、距离),计算点在椭球面上的大地坐标,或者根据两点的大地坐标,计算它们之间的大地线长和大地方位角,这样的问题就叫做大地问题解算,或称大地坐标解算。
9.表示地球椭球的大小和形状的几何参数中,a,b,e,e’,f分别表示什么意思,其公式如何表达。
长半径 a ;和短半径b ;子午椭圆的第一偏心率e;和第二偏心率e’ ;f是相对值扁率
10.写出卯酉圈、平行圈、子午圈的计算公式以及卯酉圈曲率半径公式。
卯酉圈:
\[N=\frac{a}{W}=\frac{c}{V}\]平行圈:
\[r=P K \cos B\]子午圈:
\[M=\frac{a\left(1-e^{2}\right)}{W^{3}}=\frac{c}{V^{3}}\]卯酉圈曲率半径公式:
\[N=\frac{a}{\sqrt{1-e_{1}^{2} \sin ^{2} B}}\]a是椭球长半轴;b是椭球短半轴;e1是第一离心率;B是大地纬度
11.叙述卯酉圈曲率半径和平行圈曲率半径与维度的变化规律。
12.叙述地面观测值向归算至椭球面的步骤以及相应的公式。
地面观测方向归算至椭球面:将地面观测方向归算至椭球面上,包括三个基本内容:一是将测站点铅垂线为基准的地面观测方向换算成椭球面上以法线为准的观测方向;二是将照准点沿法线投影至椭球面,换算成椭球面上两点间的法截线方向;三是将椭球面上的法截线方向换算成大地线方向。
垂线偏差改正的计算公式:
\[\begin{aligned} \delta_{1} &=-(\xi \sin A-\eta \cos A) \cot z \\ &=-(\xi \sin A-\eta \cos A) \tan \alpha \end{aligned}\]标高差改正的计算公式是:
\[\delta_{2}=\frac{\rho e^{2}}{2 M_{1}} H_{2} \cos ^{2} B_{2} \sin 2 A_{1}\]13.地面观测距离归算至参考椭球面误差改正及公式。
地面观测距离归算至椭球面:实测的电磁波测距边长在经过仪器的加常数、乘常数、大气折射、波道弯曲等项改正后,就是由仪器中心至反光镜中心间的空间直线长度,应将它归算到参考椭球面上,归算为两点间的大地线长度。公式为:
\[S=D-\frac{1}{2} \frac{h^{2}}{D}-D \frac{H_{m}}{R_{d}}+\frac{D^{3}}{24 R_{A}^{2}}\]14.将地面观测的长度归算至椭球面的计算公式可简化为(加三项改正):试说明每项改正的含义
\[S=D-\frac{1}{2} \frac{h^{2}}{D}-D \frac{H_{m}}{R_{d}}+\frac{D^{3}}{24 R_{A}^{2}}\] \[\begin{aligned} &A_{1}=A_{0}-\frac{\varepsilon^{\prime \prime}}{3}\\ &B_{1}=B_{0}-\frac{\varepsilon^{\prime \prime}}{3}\\ &C_{1}=C_{0}-\frac{\varepsilon^{\prime \prime}}{3} \end{aligned}\]第一项是测距仪与反光镜平均高程面上的水平距离;第二项是水平距离换算成椭球面上相应弦长的改正数;第三项是弦长换算成椭球面上圆弧长的改正数。
第六章 高斯投影及其计算
1.
投影变形一般分为(长度)、(面积)和(角度)三种变形。
2.
就一般的地图投影而言,长度比是一个变量,它不仅与(点位)有关,而且也随该点上线段(方向)的不同而变化。也就是说,不同点的长度比都(不同),而且同一点上不同方向的长度比也(不相同)。
3.
高斯投影的长度比M与(Ym值)有关。当高斯平面坐标Y=0时,长度比M=(1)。这是因为(中央子午线投影后长度不变)。
4.
高斯投影中,(赤道和中央子午线)投影后长度不变,而投影后为直线的有(赤道和中央子午线),其它均为凹向(中央子午线)的曲线。
5.
地图投影问题也就是建立(椭球面元素)与(椭球面)相对应元素之间的解析关系式。
6.
在地图投影分类有多种,按投影面来分,有(平面)、(圆柱面)、(圆锥面投影)等。按投影面的中心轴向来分,有(正轴(与椭球短轴重合))、(横轴(与椭球短铀正交))、(斜轴(与椭球短轴斜交)投影)。
7.
长度变形:m-1=(ds-dS)/dS ,当 m-1>0时,投影后长度将(变大);当 m-1<0时,投影后长度则(变小)。
8.
若将地球椭球面上过一点的两个互为正交的方向投影到平面上,总有一组在椭球面上正交的方向投影后仍然保持正交,则称这两个方向为(主方向)。主方向另外还有一个性质,即它们投影后具有(最大长度比)和(最小长度比)。
9.
正轴投影是圆柱面的中心轴与椭球的短轴(重合),圆柱面与椭球赤道(相切);横轴投影是圆柱面的中心轴与(椭球长轴)重合,椭圆柱面与(椭球某一子午圈)相切;斜轴投影是椭圆柱面的中心轴与椭球的长轴和短轴(都不重合),位于两者之间。
10.
将起算点的(大地坐标(B1,L1))换算成高斯投影平面上其投影点的(平面直角坐标(x1,y1)
11.
由大地方位角转换平面坐标方位角,必须先计算该大地线起点处的(平面子午线收敛角)和(方向改正)。
12.
高斯投影计算包括(高斯投影坐标计算)、(平面子午线收敛角计算)、(方向改正计算)和(距离改正计算)。
13.
将椭球面上的方向和距离归算至高斯投影平面,也就是将(大地方位角)改化为(平面坐标方位角),将(大地线长度)改化为(平面上的直线长度)。因此,需要计算(平面子午线收敛角)、(方向改正数)和(距离改正数 )
14.
方向改正就是指(大地线)的投影曲线与连接大地线两端点的弦线之间的(夹角)。
15.
高斯投影换带计算,有以下几种情况:(国家6°带坐标在相邻投影带之间的换算(6°→6°带));(国家6°带坐标换算成3°带坐标(6°→3°带));(国家3°带坐标在相邻投影带之间的换算(3°→3°带) );(国家6°带(或3°带)坐标换算成任意投影带内的坐标)。
16.
由6°带到3°带的坐标换带计算分为两种情况:一是(3°带与6°带的中央子午线重合);二是(3°带中央子午线与6°带分带子午线不重合)。
17.
高斯投影坐标的换带计算程序如下:首先将某投影带内已知点的(平面坐标(x1,y1 )),按高斯投影坐标反算公式求得其在椭球面上的(大地坐标(B,L));然后根据(纬度 B )和所需换算的投影带的中央子午线(经度 L0 ),计算该点在新投影带内的(经差 L=(l-l0)/ρ),再按高斯投影坐标正算公式该点在新投影带内的(高斯平面坐标(x2,y2))。
18.
横轴墨卡托投影属于(横轴等角割椭圆柱投影)投影, 高斯克吕格投影为(横轴等角切椭圆柱投影)投影。
19.
我国新编百万分之一地图采用(兰勃脱割圆锥)投影,按纬差4°进行分带,自赤道由南向北将我国分成(14)个投影带,采取每带的中纬和边纬的长度变形绝对值相等的条件确定(投影常熟)。
20.
高斯投影是(横轴椭圆柱等角投影),保证了投影的(角度)不变性,图形的(相似形性)性,以及在某点各方向上的(长度比)的同一性。
21.
兰勃脱投影是(等角正圆柱投影(投影,它的长度变形(m-1)与(经度)无关,但随纬差 ,即纵坐标 的增大而迅速(增大),为限制长度变形,采用按纬度的分带投影。
22.名词解释
- 地图投影 通过投影方法将椭球面上的测量元素——大地坐标、大地线长度和方向以及大地方位角等归算到投影平面上。这部分内容通常称为地图投影,简称为投影
- 投影变形 :椭球面上的元素(如一段距离、一个角度、一个图形)投影到平面上,也就会和原来的距离、角度、图形呈现差异,这一差异称作投影变形。
- 投影长度比 : 就是投影平面上的微分线段ds与椭球面上该线段实际长度dS之比,以m表示。
- 等量纬度 : 只与大地纬度B有关,故可把dq和dL看作互为独立的变量的微分。
- 高斯投影 :又称横轴椭圆柱等角投影,属于正形投影。
- 高斯平面直角坐标系 :在高斯投影平面上,中央子午线和赤道的投影都是直线。若以中央子午线与赤道的交点O作为坐标原点,以中央子午线的投影为纵坐标轴,即x轴,以赤道的投影为横坐标轴,即y轴,这就形成了高斯平面直角坐标系。
- 高斯坐标正算 :由大地坐标推求高斯平面坐标。
- 高斯坐标反算 :由高斯平面坐标推求大地坐标。
- 子午收敛角 :坐标纵线偏角,以真子午线为准,真子午线与坐标纵线之间的夹角。坐标纵线东偏为正,西偏为负。在投影带的中央经线以东的图幅均为东偏,以西的图幅均为西偏。
- 距离改正 :将椭球面上的大地线长度S改化为高斯投影平面上投影曲线两端点间的弦长D,称为距离改正。
23.叙述高斯投影的计算内容及其公式。
- 高斯投影坐标计算:将起算点的大地坐标(B1,L1),换算成高斯投影平面上其投影点的平面直角坐标(x1,y1),称为高斯投影坐标计算。
- 平面子午线收敛角计算:将起算边的大地方位角A12,换算成高斯投影平面上的平面坐标方位角T12。用y表示坐标北方向l’t相对于真北方向l’n构成的夹角,称作l’的平面子午线收敛角。
- 方向改正计算:根据上述过程再用δ12表示投影曲线的弦线相对于投影曲线构成的夹角,称为方向改正。T12与A12之间的关系为 \(T_{12}=A_{12}-\gamma+\delta_{12}\) 因此,若由大地方位角转换平面坐标方位角,必须先计算该大地线起点处的平面子午线收敛角和方向改正。
-
距离改正计算:将起算边的大地线长度S12归算至高斯平面上的直线长度D12。 \(D_{12}=S_{12}+\Delta S\) 式中, ΔS是由大地线长度改化为高斯平面上直线长度时加入的改正数,称为距离改正。
- 统称为高斯投影计算:对于椭球面上三角网的各观测方向和边长分别进行方向改正和距离改正,归算至高斯投影平面上的直线方向和直线距离,组成由平面三角形构成的三角网,进行平差计算,解算平面三角形,推求各控制点的平面直角坐标。
24.简述什么叫距离改化。在什么情况下需要进行距离改化计算。
将椭球面上的大地线长度S改化为高斯投影平面上投影曲线两端点间的弦长D ,称为距离改正。D与 S的差异,就是距离改正数 ΔS。将地面测量的距离换算到高斯投影平面,或根据高斯平面上的长 度换算为实地距离时,都需要计算这个距离改正数。
25.简述为什么要邻带换算。如何进行邻带换算。
- 当控制网位于两个相邻投影带的边缘地区并横跨两个投影带,为了能在同一带内进行平差计算,必须把控制网起算点的坐标换算到同一个投影带内。
- 在分带子午线附近地区测图或进行测量工程时,往往需要用到另一带内的控制成果,因此,也需要将这些点的坐标换算到同一带内。
- 当大比例尺测图时,特别是在工程测量中,为了限制投影变形,常要求采用3°带、1.5°带或任意带投影,而国家控制点成果通常只有6°带坐标,这时就产生了6°带与3°带(或1.5°带、任意带)之间的相互坐标换算问题。
首先将某投影带内已知点的平面坐标(x1,y1),按高斯投影坐标反算公式求得其在椭球面上的大地坐标(B,L);然后根据纬度B和所需换算的投影带的中央子午线经度L0,计算该点在新投影带内的经差(l=(L-L0)/ρ),再按高斯投影坐标正算公式该点在新投影带内的高斯平面坐标(x2,y2)。



