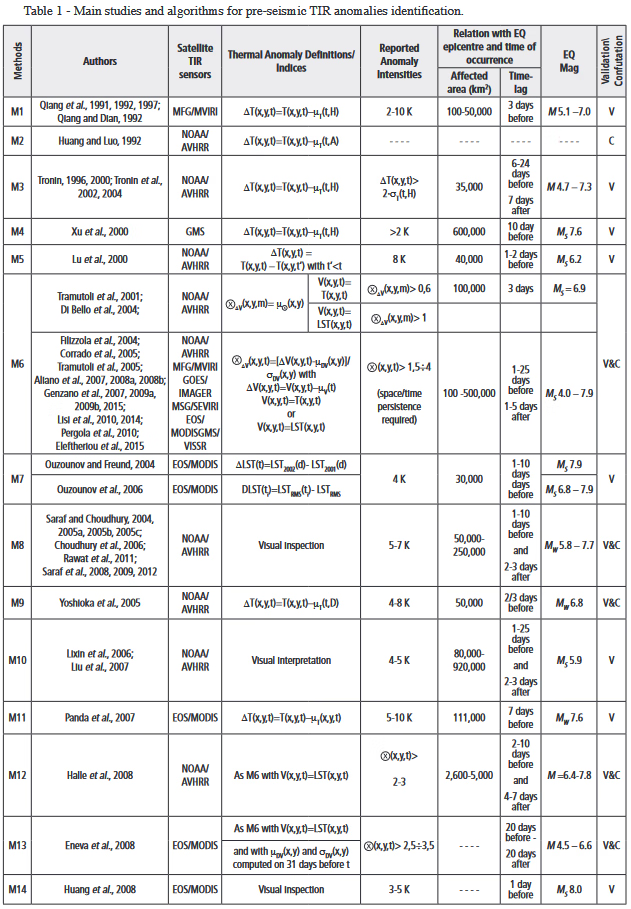
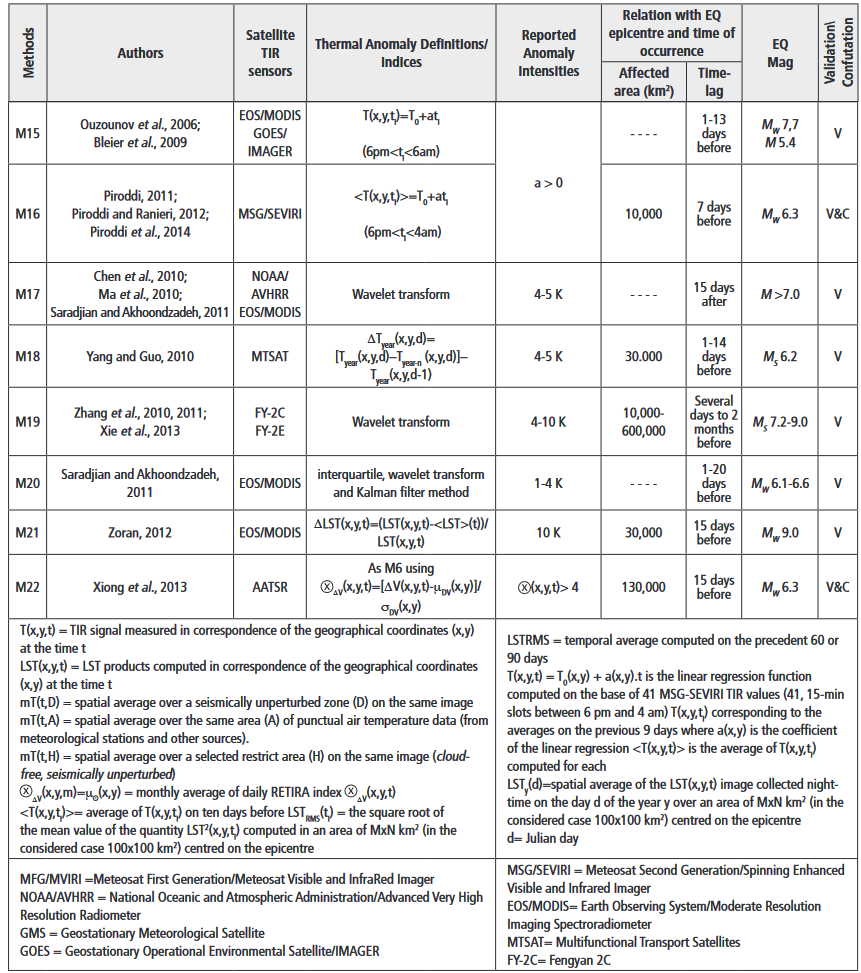
案例
| 论文 | 作者 |
|---|---|
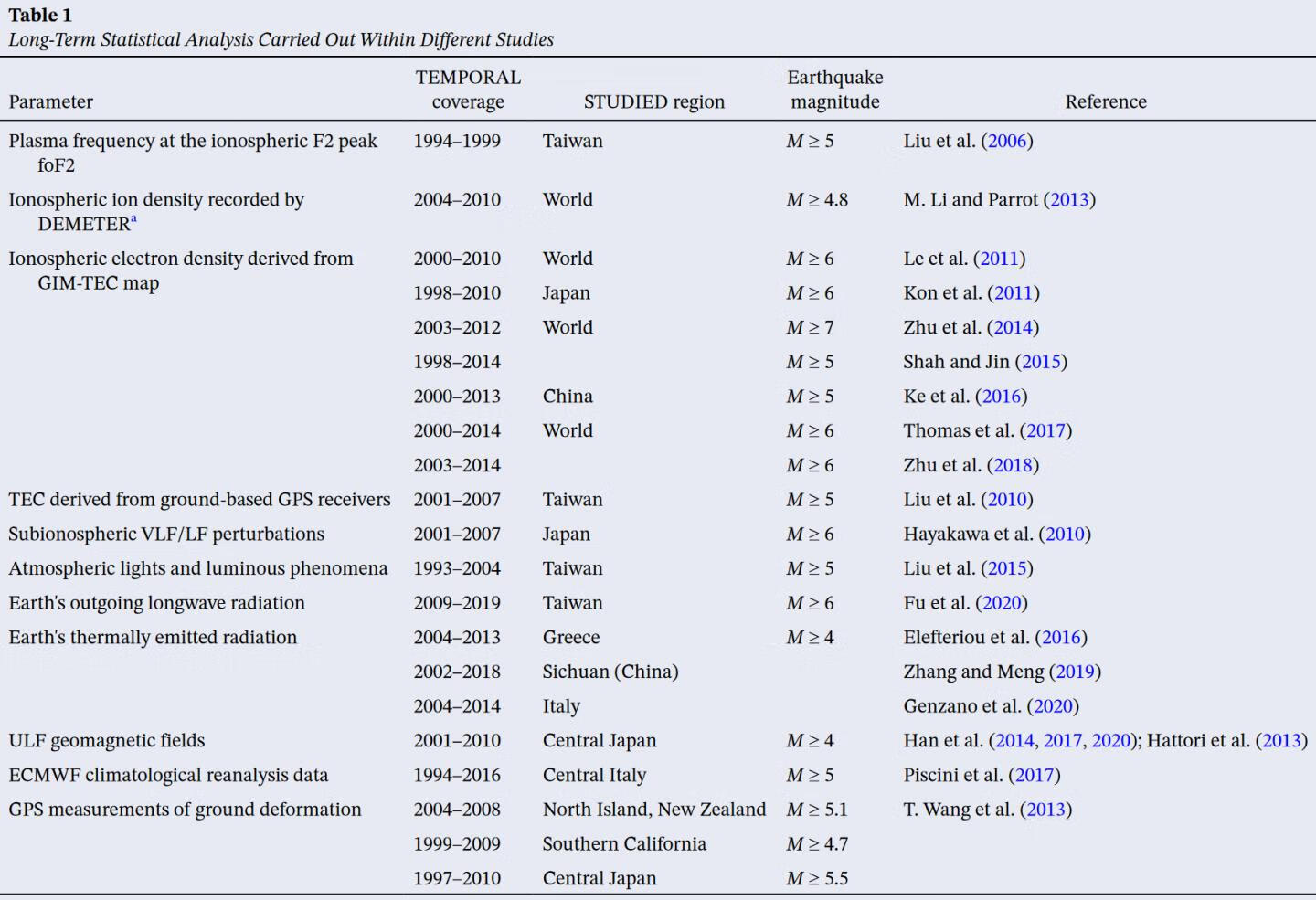
| Statistical Correlation Analysis Between Thermal Infrared Anomalies Observed From MTSATs and Large Earthquakes Occurred in Japan (2005–2015) | N. Genzano and V. Tramutoli |
本文作者提供的其他不同的研究状况,供参考。
1.数据和方法
通过分析MTSAT-1R卫星上的JAMI传感器在2005年6月至2010年6月期间以及MTSAT-2卫星上的IMAGER传感器在2010年7月至2015年12月期间以10.8微米(10.3-11.3微米)获取的所有夜间(00:30 LT;即15:30 UTC-1天)TIR图像,确定了热异常。这些图像属于千叶大学CEReS提供的空间分辨率为0.04°的网格化数据集。
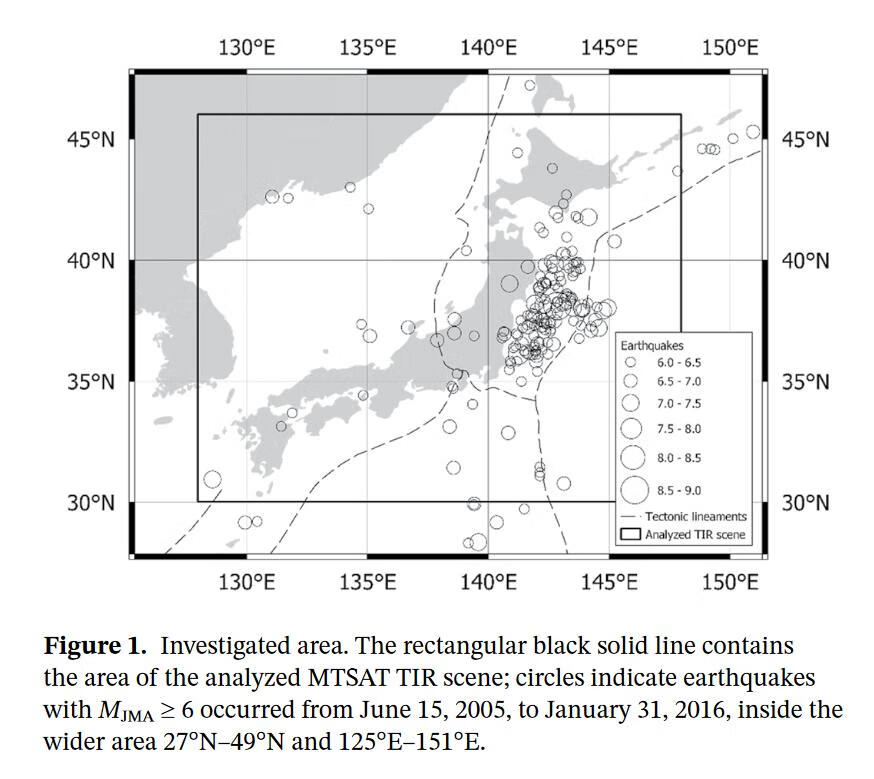
图1显示了调查区域(北纬30-46°,东经128-148°),该区域涵盖了日本领土。这里还显示了2005年6月15日至2016年1月31日期间发生在比调查区域大3°的地区的地震。根据日本气象厅的地震目录(日本气象厅,2021年),有229个MJMA≥6的事件和79个MJMA≥6.5的事件,发生在所考虑的时间段和选定的地理区域。
在这项研究中,为了识别TIR异常,使用了基于统计学的TIR异常估计器(RETIRA;Filizzola等人,2004;Tramutoli等人,2005)指数,在Genzano等人(2020)称为RETIRAbox

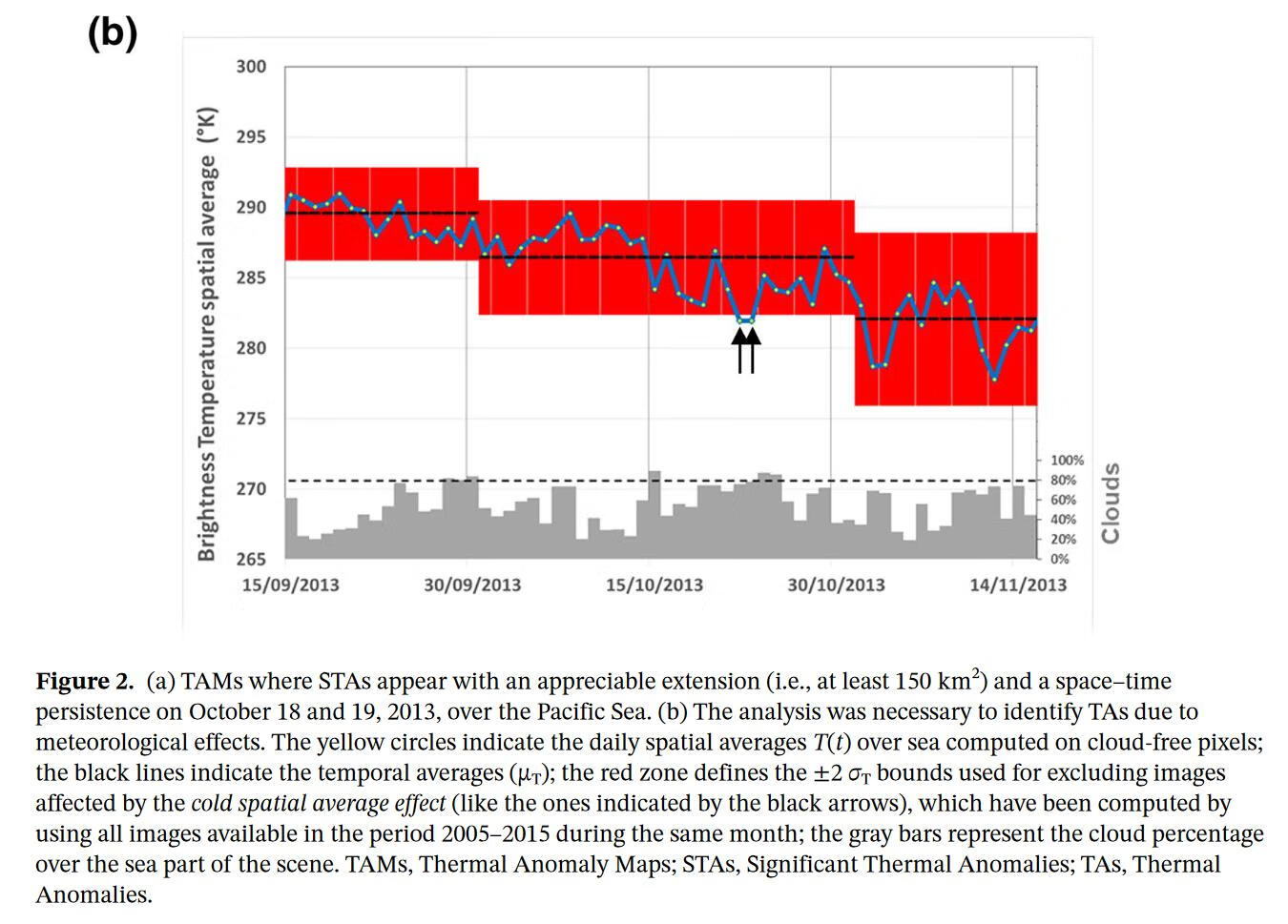
作者在这里采用了Eleftheriou等人(2016)提出的改进的RST预处理阶段,以减少气象云对参考场计算可能产生的负面影响以及随之而来的可能的假阳性的扩散。事实上,在日本这样的地理环境中,这种影响可能特别大,因为在一个相对较小的土地范围内,受到各种气候条件的影响。此外,它还受到一些现象的影响,如夏季和初秋时南部的季风,8月至10月太平洋一侧的台风,以及日本海北部鄂霍次克海大气压力的影响。

Significant Sequence of Thermal Anomalies (SSTAs)需满足以下条件:

2.数据分析
2.1地震目录过滤
地震集群可能对结果有影响,地震目录的解聚是一个基本的初步分析,其质量可能影响后续分析的结果。
在这项研究中,采用了特定的标准来选择相关分析中考虑的地震。由于相邻地区在一个时间跨度ts中可能发生不止一次地震,对于在ts中发生的每个地震事件:
(a)我们计算了相应的Dobrovolsky半径(Dobrovolsky等人,1979),其中Mi是第i次地震的震级; (b)我们按照震级的大小和发生时间的递增进行排序; (c)从列表中的第一个震例开始,我们排除了所有落在其Dobrovolsky半径内的震例; (d)我们对列表中所有幸存的震例重复这个过程,直到所有的震例都被评估过。
对于这项研究,我们生成了两个不同的过滤目录:
- Daily filtered catalog, where ts = 1 day. We used this catalog for a preliminary evaluation of comparative performance between the traditional RST analysis and its optimized arrangement, here presented. This filtered catalog consists of 157 events with MJMA ≥ 6 and 58 events with MJMA ≥ 6.5.
- Monthly filtered catalog, where ts = ±30 days. We used this catalog to evaluate if the high seismicity of the Japanese region could affect results concerning the RST-optimized arrangement. This filtered catalog consists of 82 events with MJMA ≥ 6 and 35 events with MJMA ≥ 6.5.
2.2基于RST的TIR异常与地震(MJMA≥6)发生的相关性分析
我们将上述规则应用于2005年6月至2015年12月期间的所有MTSAT TIR图像,并确定了60个SSTA(分布在132个不同的TIR图像上,即占所有可用TIR图像的3.5%)。
我们评估了SSTA的出现与属于每日过滤目录的地震的位置、时间和震级之间可能的相关性。为此,我们应用了经验规则,这些规则是在考虑到以前的研究(见Tramutoli, Corrado, Filizzola, Genzano, Lisi, & Pergola, 2015; Tramutoli et al., 2018, and references therein)和迄今为止提出的解释大地震前后TA出现的物理模型(如Tramutoli et al., 2013)后建立的。此外,定义的验证规则,应驱动回顾性的相关分析,与CSEP项目(Schorlemmer等人,2018)使用的规则相匹配。
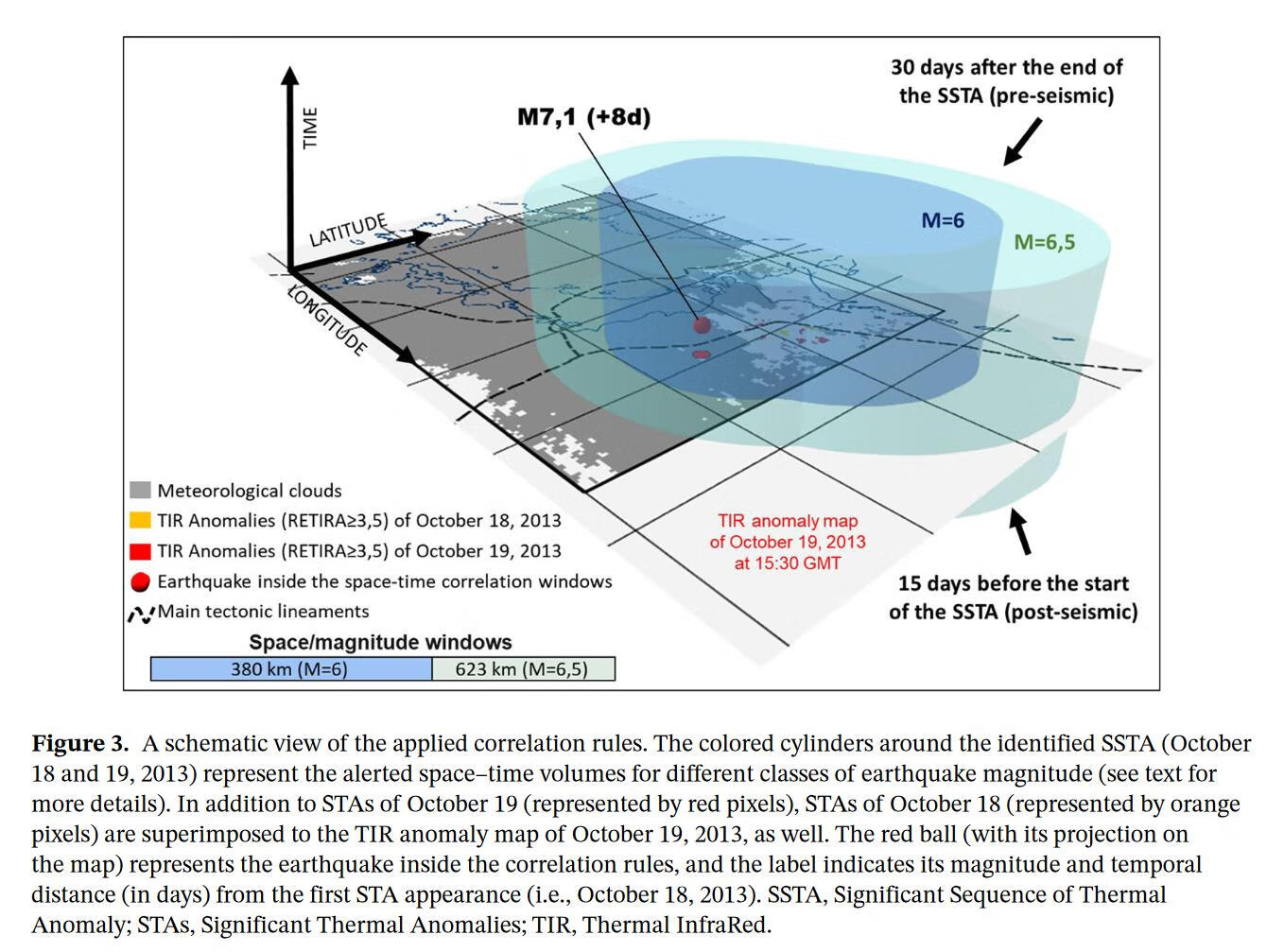
按照这样的规则,我们认为在一个地理位置(x,y)上观察到的每一个STA,在时间t,并且属于先前确定的SSTA,与M≥6的地震事件相关,如果它发生在规定的范围内:
- 时间窗口,即在(震前异常)最后一次出现TA后30天内,或直到(震后/地震异常)第一次出现TA前15天内。
- 空间窗口,即与形成SSTA的TA的距离RD内,其中RD=10^0.43M,即Dobrovolsky半径(Dobrovolsky等人,1979)。
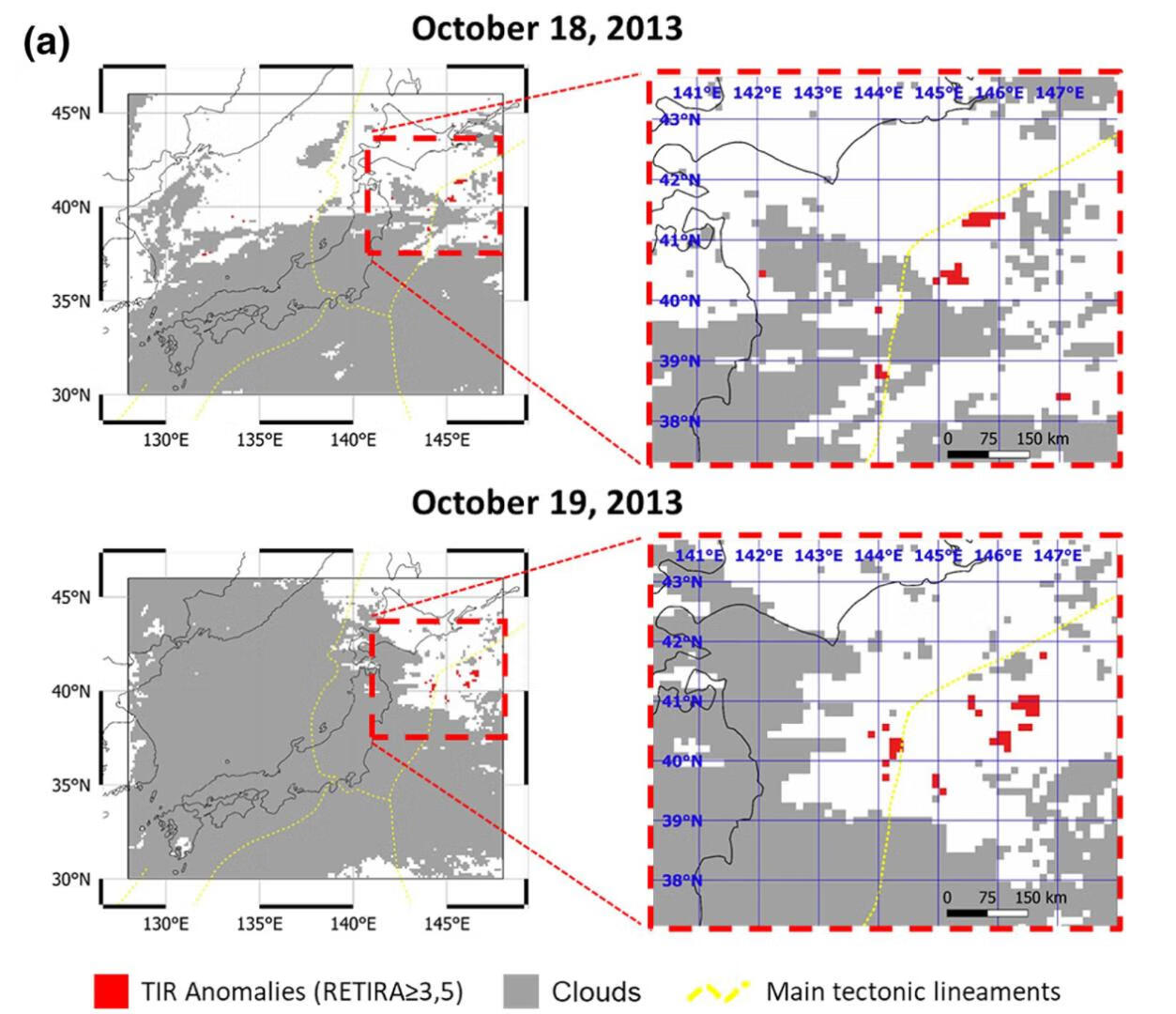
图3显示了应用规则的示意图。对于2013年10月18-19日的SSTA,为验证TA和地震事件之间的可能关系,对不同级别的地震震级定义了一个时空体积(这里只有M≥6和6.5的地震用不同颜色表示)。满足上述定义的地震为红点。在这种情况下,2013年10月18日和19日在日本东北海岸出现的STA,之后发生了一次7.1级的地震。它发生在太平洋上第一次出现的TA之后8天(即2013年10月26日)。
2.3减少假阳性TIR异常的发生
在本文中,我们提出了一个不同的标准来计算RST参考场。我们没有使用FWC(fixed-monthly window criterion),而是在一年中每个被分析的日子周围使用了30天的时间窗口(即±15天)(移动窗口标准,MWC)来建立(366×2而不是12×2)参考场。通过这种方式,我们计算了732幅参考场图像(一年中的每一天都有两幅,μ和σ,图像),而不是24幅月度参考场图像(一年中的每个月都有两幅,μ和σ,图像)。这使我们能够将TIR记录与最合适的参考场进行比较。在一年中的某些地理区域和时期,这种选择可以大大减少发生在月初/月末的热异常现象的扩散。沿着上述步骤,我们对SSTA和属于每日过滤目录的地震进行了新的相关分析。使用以前用于评估RSTFWC性能的相同目录,使我们能够更好地判断RSTMWC与RSTFWC相比所取得的改进。
这项新的分析强调,在2005年6月至2015年12月期间,在日本地区的29个确定的SSTA(在这种情况下,分布在69个不同的TIR图像上,即占全部可用TIR图像的1.8%)中,有62.1%显然在空间和时间上与报告的地震事件有关(MJMA≥6)。
比较两个独立的 RST 分析,应关注以下方面的减少:

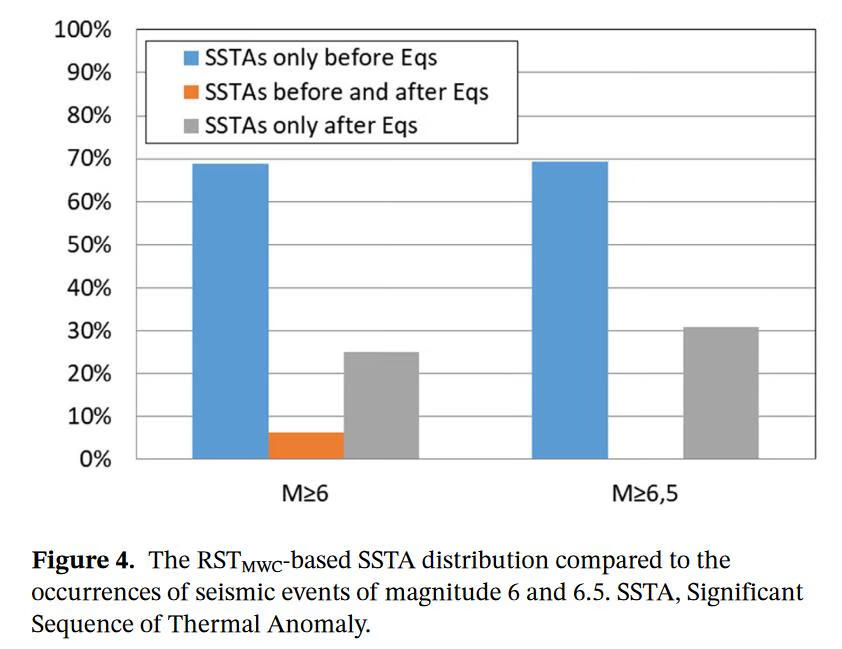
震前SSTA占主导地位
我们进行了随机测试分析,目的是评估所取得的结果的质量和 “基于RST的卫星热异常 “参数对专门用于评估短期地震危险的多参数系统的潜在信息贡献。这种分析还应该强调,如果SSTA(包括事件前和事件后)看起来与地震有关,只是因为所研究地区的高地震率和/或因为使用的相关空间/时间规则(最终设置得太大)。
我们考虑了Molchan方法(Molchan,1997年,以及其中的参考文献),作为验证基于SSTA的实际值的参考方法,与基于随机的报警函数相比。
根据所调查参数的具体特征(即基于 RST 的 SSTA)采用 Shebalin 等人提出的定制 Molchan 误差图。 (2006),而不是使用基于似然检验的方法。

同时,作者还计算了概率增益(Aki,1989)G=(1-νEQ)/τSSTA,以及基于无效假设的置信极限曲线(详见Kossobokov,2006),在随机猜测的对角线周围95%的水平。
误差图结果如下图。

图5(a)显示,从事件的角度来看,警报已经被证明比随机猜测要好,但为了验证从警报的角度来看是否相同,我们建立了一个特设的错误图(图5(b)),考虑到


计算了震级≥M的地震所占据的时空域,其中:
- 时间窗口:从地震发生前30天到地震发生后15天(共46天)。
- 空间窗口: RD=10^0.43M,即Dobrovolsky半径(Dobrovolsky等人,1979)。
图5(b)强调,即使从报警的角度来看,SSTA也优于随机猜测。同样在这个测试中,概率增益被计算为G=(1-νSSTA)/τEQ。与随机猜测相比,获得的数值达到2.95(对于M≥6的地震之前的SSTA)。
作者还评估了地震群对所取得结果的可能影响(在Michael[1997]中也有讨论)。为了达到这个目的,我们保留了SSTA的空间特征和它们的时间长度,同时随机生成了每个SSTA的起始时间。通过这种方式,我们生成了50个合成SSTA的集合。图6(b)显示了Molchan分析的结果(只报告了在合成SSTA上取得的结果的平均值)。
这种分析的平均值(图6(b))和所有的结果(见辅助资料中的表S4)都落在误差图的不乐观区域;它们都在显著水平α=5%下拒绝了空假设。

3.多参数方法
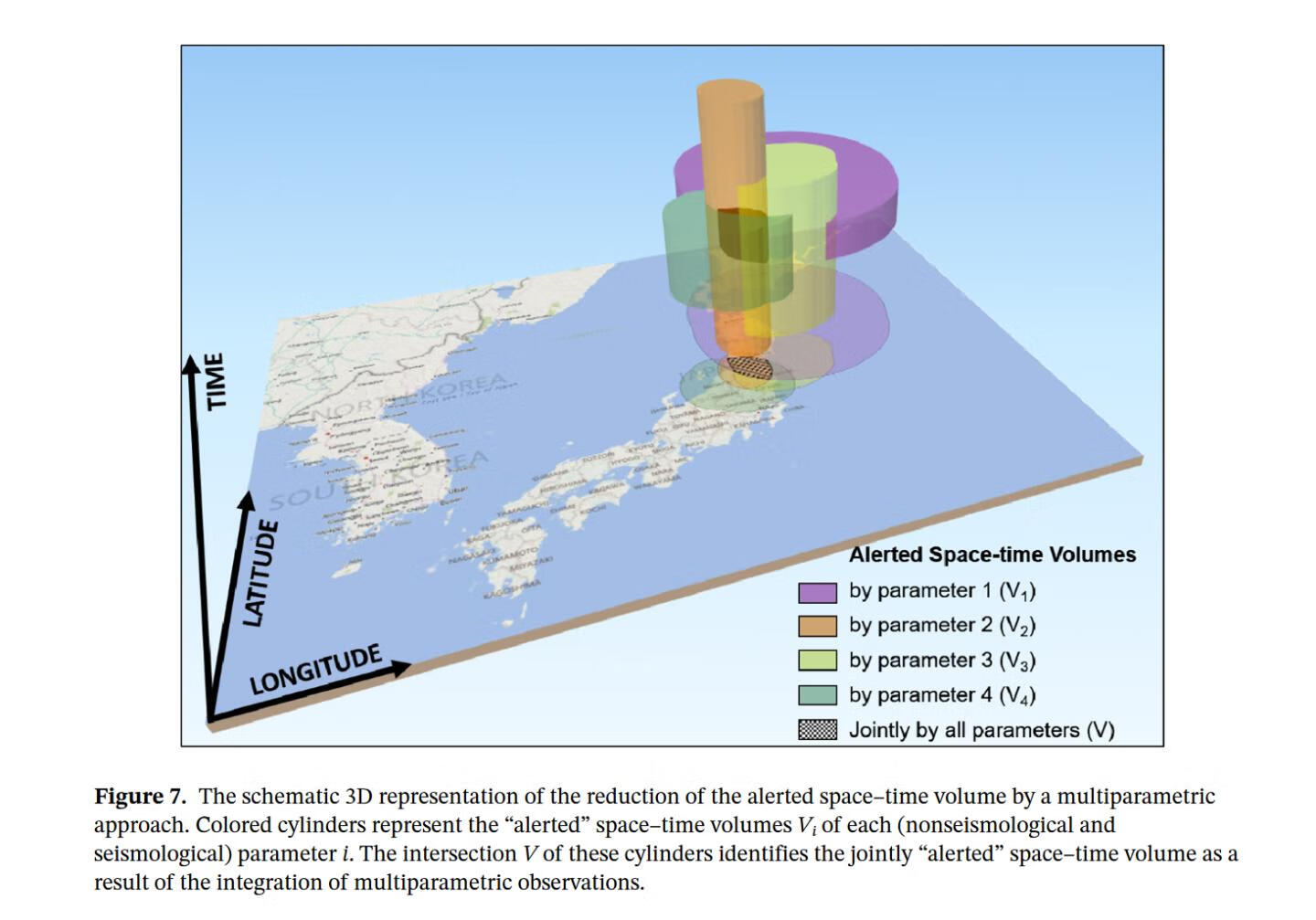
4.扩展
4.1震前TIR异常提取主要研究和算法