对中长期地震危险性概率预测结果的统计检验是地震预测预报的重要研究内容，采用通用的统计检验方法是租金地震预测理论、模型“无障碍”交流和发展的必要条件。最近在阅读统计地震学相关论文时，经常碰到Molchan diagram方法，用以评估地震预测模型的优劣。正好我导师发给我一篇关于该方法的中文介绍，在此记录一下。

Molchan图表法涉及的变量有：

• h-击中数(Hits)：预测“有震”而实际发震的地震数／空间网格
• H-击中率(HitRate)：预测“有震”而实际发震的地震数／空间网格数与总的实发地震数／所占空间网格数之比
• v-漏报率(MissRate)：预测“无震”而实际发震的地震数／空间网格数与总的实发地震数／所占空间网格数之比
• τ-异常的时空占有率(FractionofSpace-timeOccupiedbyAlarm)：发出预测“警报”的时空范围与总的时空范围之比

Molchan图表法使用τ和v来进行统计评分,最佳的预测效果对应在最大预测成功（v→0）下付出最小的代价（τ→0）。τ在计算中常根据预测检验策略或要求的不同,进行加权处理。将空间G划分成等尺寸、不重叠的网格（Gi,i＝1,…,k）,加权后的“异常时空占有率”τw可表示为:

$\tau_w=\sum_{i=1}^k w_i \tau_i, \sum_{i=1}^k w_i=1, w_i \geqslant 0$

式中,k为网格数,wi为网格i的权重。在这里，wi可根据预测策略和目标的不同采用不同的表示形式，例如采用网格面积比、空间G内“目标地震”的发生率等形式。

一般情况下，可以通过计算(τ，v)曲线与Molchan图表的边界线τ=0和v=0所包围的面积来评估地震预测模型的效果，面积越小则预测效果越好；同时，还需要考察“击中数”h所对应显著性水平。由于总数为N次事件中有h次或h次以上事件“击中”的分布概率可写为二项式形式，相应的显著性水平α值可计算如下：

$\alpha=\sum_{i=h}^N\left[\left(\begin{array}{c}N \ i\end{array}\right) \tau^i(1-\tau)^{N-i}\right],\left(\begin{array}{c}N \ i\end{array}\right)=\frac{N !}{i !(N-i) !}$

式中，N为地震数。在Molchan图表中绘制α＝1％、α＝5％、α＝25％和α＝50％的等值线，通过τ～v曲线上各点与各显著性水平α等值线的比较‚也可判断预测的效果。由上式也可见，α等值线的位置是与实际发生的地震数N有关。

Molchan图表法的概率增益被定义为：

$\operatorname{Gain}=\frac{H}{\tau}=\frac{1-\nu}{\tau}$

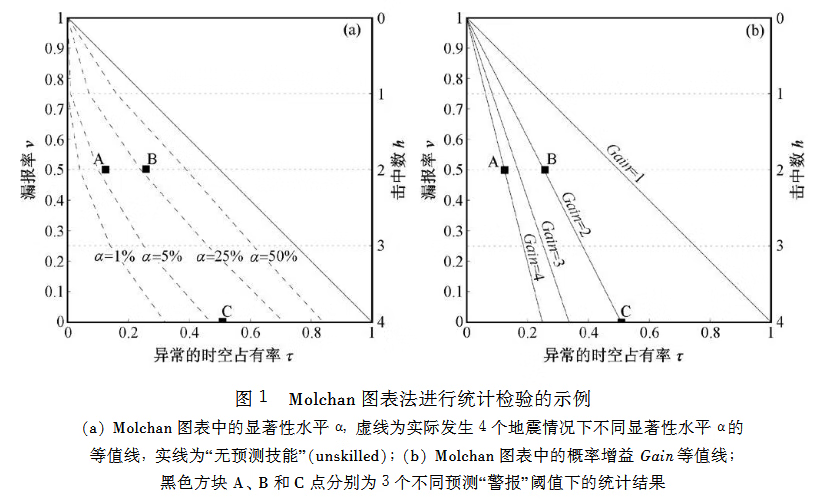
由此可见，概率增益Gain在图表中即为（0,1）至（τ,v）连线的斜率，而当连线为（0,1）至（1,0）的直线时Gain＝1,表示预测方法无统计显著性。图1给出了实际发生4个地震情况下，利用Molchan图表法进行统计检验的示例，其中图1（a）给出了不同显著性水平α的等值线，图1（b）给出了不同概率增益Gain的等值线。对于图1中的A、B和C三点，可通过与α等值线和Gain等值线判断各自的预测效果。例如，B和C点具有相同的概率增益，但B点的置信水平低于C点；A点置信水平和概率增益明显优于B点。

参考论文

[1]蒋长胜, 张浪平, 韩立波,等. 中长期地震危险性概率预测中的统计检验方法Ⅰ:Molchan图表法[J]. 地震, 2011, 31(2):8.

原文可点击查看：中长期地震危险性概率预测中的统计检验方法_ⅠMolchan图表法_蒋长胜.pdf