该方法是基于Molchan diagram方法的改进，Molchan diagram简介可看上文：Molchan图表法。以下内容均为原作者提出的观点，本人没有做任何观点上的修改。

背景

原始 Molchan diagram 仅仅只对事件漏报率进行了检验，忽略了警报成功率 的重要性。对于一组警报，只关注事件漏报率或警报成功率是不够的，从地震预报 实际角度出发，警报成功率过低，警报可信度太差，过多的误报类似于“狼来了”； 而过低的事件漏报率则代表极大的未知威胁。这促使本研究构建一个同时考虑警报 成功率与事件漏报率，更为全面的警报性能评估模型。该模型可对警报的事件漏报 率与警报成功率分别进行显著性检验，并针对多指标给出定量化评估，为后续构建 前兆提取模型提供必要的有效性检验手段。

针对事件漏报率的显著性检验

地震与前兆并非“一对一”而是“多对多”的对应关系，为全面评估警报性能，分别从事件和警报角度出发，引入如下定义：

• TP1: True positive 1，与地震对应的前兆数量。
• FP: False positive，不与地震对应的前兆数量。
• TP2: True positive 2，与前兆对应的地震数量。
• FN: False negative，不与前兆对应的地震数量。
• PPV: Positive predictive value，前兆预测成功率，即与地震对应的前兆数量占总前兆的比例。
• FDR: False discovery rate，前兆预测失败率，即不与地震对应的前兆数量占总前兆比例。
• TPR: True positive rate，事件的真阳性率，即与前兆对应的事件数量占总事件的比率。
• FNR: False negative rate，事件的漏报率，即不与前兆对应的事件数量占总事件的比率。

在对警报进行评估时，首先要确保警报在事件漏报率以及警报成功率上均优于随机猜测，因此首先要对警报的事件漏报率和警报成功率分别进行显著性检验。事件漏报率的 p-value 如下式所示：

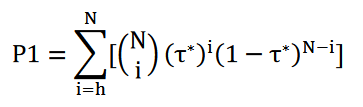
原假设H0：该组警报的事件漏报率与随机猜测无异。当P1 ≪ α，且α ≪ 1时，拒绝原假设，即该组警报从事件漏报率角度要优于随机猜测。

针对警报成功率的显著性检验

原文过于复杂，不做介绍，详情参考原文。

3D Molchan diagram

原始的 Molchan diagram 是事件漏报率关于时空预警区域的函数，只考虑了事件的漏报率而忽略了警报的成功率。然而优秀警报应当是以最小的预警时空域，准确预报更多的事件，同时要保持尽可能高的警报成功率。为满足上述理念，在原始标准的 Molchan diagram 中引入第三个轴用以包含警报的警报成功率信息。3D Molchan diagram 的 x 轴和 y 轴分别代表警报时空域占总时空域的比例τ或 Spatialtemporal correlation window (STCW)以及事件漏报率，新增的 z 轴则为警报误报率 (FDR)，FDR=1-PPV。此外，3D Molchan diagram 中还包括针对于事件漏报率和警报成功率的显著性检验，如上文所示。在 3D Molchan diagram 中，最优警报位于原点(0,0,0)代表着该组警报中无误报且无漏报。理论上 x 轴所代表的警报时空域占总时空域的比例是无法等于 0 的，但是随着地震预测预报研究的发展，STCW 会无限接近于0。为评估警报性能，重新定义评估分数如下：

$\operatorname{Loss}=\sqrt{\mathrm{w}_1 * \mathrm{STCW}^2+\mathrm{w}_2 * \mathrm{FNR}^2+\mathrm{w}_3 * \mathrm{FDR}^2}$

上式中 Loss 实际上是(STCW, FNR, FDR)到原点的加权距离，(w1, w2, w3)是根据这三个指标设置的权重，通常w1 = w2 = w3 = 1。（这些权重的设置取决于不同策略的微妙权衡-为最小化警报成本或最 大化与警报相关的地震数量，需要根据社会人民安全和经济考量对警报成功率、事 件漏报率和预警时空域进行加权，但是如何确定最优预测策略是一个涉及社会学、 经济学、伦理学等诸多学科的复杂而富有挑战性的课题，值得深入研究。）在 3D Molchan diagram 中，Loss越高则警报越差。根据事件漏报率的显著性检验结果P1、警报成功率的显著性检验结果P2以及显著性水平α = 0.05，对警报进行如下分类：

• I 类警报：P1≤0.05 且 P2≤0.05。该警报无论从警报成功率或事件漏报率角度都优于随机猜测，是最为理想的警报种类。
• II 类警报: P1>0.05 且 P2≤0.05。该组警报从警报成功率角度是有效的，代表着当警报发生时，人们可以相信并且根据警报进行避险。但是，其在事件漏报率上较差表现会使得人们受到更多漏报事件的威胁。
• III 类警报: P1≤0.05 且 P2>0.05。该组警报从事件漏报率角度是有效的，依据该组警报人们可以尽可能多地避免地震灾害带来的危险，但在警报成功率上较差表现使得其可信度较差。
• IV 类警报：P1>0.05 且 P2>0.05。该组警报无论从警报成功率还是事件漏报率对于地震的预测都无效。

参考论文

[1]张颖. 基于热红外异常的中国大陆地震预测研究[D]. 中国科学院大学.